11726


위 문제를 그림으로 나타내면 아래와 같다.

이와 같이 2*n의 타일을 2*1과 1*2 타일로 채워넣으면 되는 것이다.
처음 다이나믹 프로그래밍을 배우고 푸는 문제라 직접 경우의 수를 다 따져가며.. ㅎㅎ.. 풀려고 했었다.. (삽질)
이는 너무 복잡하게 생각할 필요없이 아래와 같이 풀면 된다.

말로 설명해보면, 2*n의 타일을 채우는 것은 결국 2*n-1의 타일에 2*1을 하나 붙인 것과 2*n-2 타일에 1*2 타일을 두개 붙인 것과 같기 때문에, 이를 점화식으로 쓰면 D[n] = D[n-1] + D[n-2] 과 같게 된다.
이를 코드로 작성하면 아래와 같다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
int t[1001];
int tile(int n) {
if (n == 1)
return 1;
if (n == 2)
return 2;
else if (t[n] != 0)
return t[n];
return t[n] = (tile(n - 1) + tile(n - 2)) % 10007;
}
int main() {
int n;
scanf("%d", &n);
if (n == 0)
return 0;
printf("%d", tile(n));
return 0;
}
|
cs |
그럼 이제 이와 비슷한 11727을 풀어보도록 하자.
11717


위 문제를 그림으로 나타내면 아래와 같다.

11726과 같은 경우에서, 2*2 타일로 채우는 경우가 추가한 것이다.
이 문제는 아래와 같이 풀 수 있다.
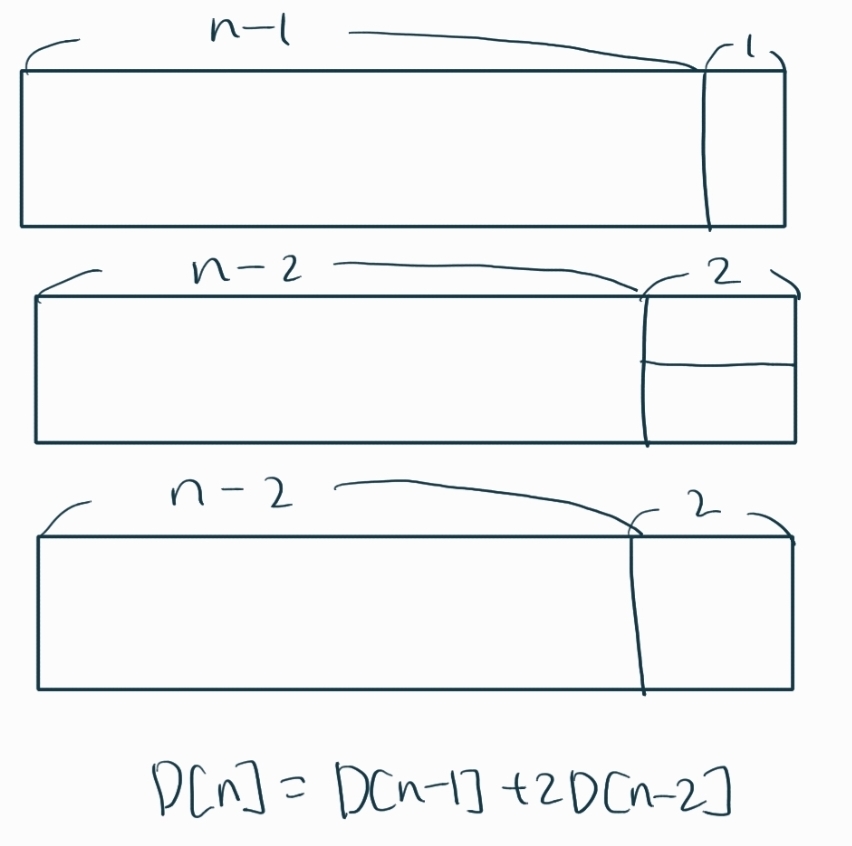
말로 설명해보면, 2*n의 타일을 채우는 것은 결국 2*n-1의 타일에 2*1을 하나 붙인 것과 2*n-2 타일에 1*2 타일을 두개 붙이거나 2*2 타일을 하나 붙이는 것과 같기 때문에, 이를 점화식으로 쓰면 D[n] = D[n-1] + 2*D[n-2] 과 같게 된다.
이를 코드로 작성하면 아래와 같다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
int t[1001];
int tile(int n) {
if (n == 1)
return 1;
if (n == 2)
return 3;
else if (t[n] != 0)
return t[n];
return t[n] = (tile(n - 1) + 2*tile(n - 2)) % 10007;
}
int main() {
int n;
scanf("%d", &n);
if (n == 0)
return 0;
printf("%d", tile(n));
return 0;
}
|
cs |
그럼 이를 토대로 조금 더 심화문제 2133을 풀어보자
2133


위 문제도 그림으로 나타내면 아래와 같다.

앞서 두 문제와 다른 점이 있다면, 2*n 이 아니라 3*n인 것이다.
이 문제는 아래와 같은 방식으로 해결할 수 있다.


말로 설명해보면, 3*n의 타일을 채우는 것은 결국 3*n-2의 타일에 세가지의 경우로 3*2를 채우는 경우와
3*n-4 타일에 그림과 같은 경우로 3*4를 채우는 경우로 나뉠 수 있다. 그러나 이 문제인 경우, 앞서 말한 n-4일 때와 같이 n-a에서 a가 4이상의 짝수일때 2가지의 경우가 더 생기므로, 이를 점화식으로 나타내면
D[n] = 3*D[n-2] + (2*D[n-4]+2*D[n-6]+...+2*D[0])
와 같게 된다.
이를 코드로 작성하면 아래와 같다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
int t[31];
int tile(int n) {
int result = 0;
if (n == 0)
return 1;
if (n == 1)
return 0;
if (n == 2)
return 3;
else if (t[n] != 0)
return t[n];
result = (3 * tile(n - 2));
for (int i = 3; i <= n; i++) {
if (i % 2 == 0)
result += 2*tile(n - i);
}
return t[n] = result;
}
int main() {
int n;
scanf("%d", &n);
printf("%d", tile(n));
return 0;
}
|
cs |
이렇듯 오늘은 dp 3문제를 풀어보았다(사실 풀기는 한참 전에 풀었다)
dp를 모른채로 듣기만 하였을때는 먼가.. 이름이 어려워보였는데 막상 해보니 할만 한 거 같다 (걍 쉬운 문제라 그럴수도)
아무튼 앞으로 이를 참고해서 dp와 관련된 문제를 몇개 더 풀어봐야겠다는 생각이 들었다.