소수판별 - 에라토스테네스의 체

에라토스테네스의 체

에라토스테네스의 체는 가장 대표적인 소수 판별 알고리즘이다. 에라토스테네스의 체는 소수를 대량으로 빠르고 정확하게 구하는 방법이다. 그럼 먼저 소수 판별 알고리즘을 살펴보자.

 

#include <stdio.h>
#include <math.h>
 
bool isPrimeNumber(int x) {
    int end = (int)sqrt(x);
    for (int i = 2; i <= end;i++) {
        if (x % i == 0)
            return false;
    }
    return true;
}
 
int main() {
    printf("%d", isPrimeNumber(97));
    return 0;
}
 

위와 같은 경우 약수는 2*4=4*2 처럼 대칭을 이루기 때문에 제곱근까지만 약수의 여부를 검증하였으므로, O(N^(1/2))의 시간 복잡도를 가진다.

 

그럼 이렇게 한개의 수에 대한 소수 판별이 아닌 대량의 소수를 한꺼번에 판별하고자 할 때는 어떤 알고리즘을 사용해야 할까? 바로 이때 사용하는 것이 에라토스테네스의 체이다.

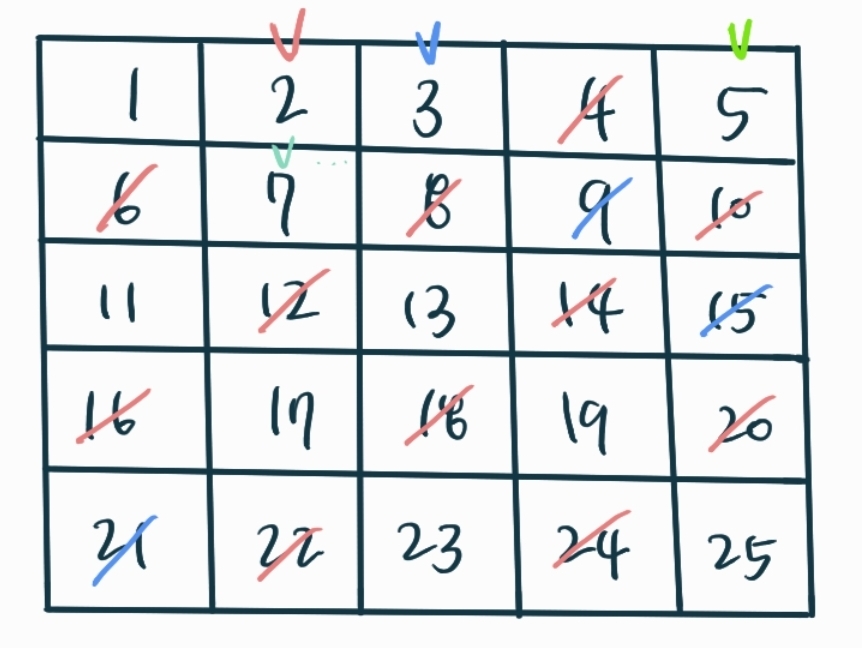
에라토스테네스의 체는 다음과 같다. (1부터 25까지의 수 중 소수 판별한다고 가정)

 

1. 이차원 배열을 생성하여 값을 초기화한다.

2. 2부터 시작해서 특정 숫자의 배수에 해당하는 숫자들을 모두 지운다. 이때, 이미 지워진 숫자인 경우 건너뛴다.

3. 그 후 2부터 시작하여 남아있는 숫자들을 출력한다.

 

이렇게 되면 1~25일때 출력값이 2,3,7,11,13,17,19,23 으로 1~25 사이의 소수가 출력값으로 나오게 된다.

이를 그림으로 나타내면 아래와 같다.

그럼 이를 코드로 작성해보자.

 

#include <stdio.h>
 
int n = 10000;
int a[10001];
 
void primeNumberSieve() {
    for (int i = 2;i <= n;i++)
        a[i] = i;
 
    for (int j = 2;j < n;j++) {
        if (a[j] == 0) continue;
        for (int i = j + j;i <= n;i += j) {
            a[i] = 0;
        }
    }
 
    for (int i = 2;i <= n;i++) {
        if (a[i] != 0)
            printf("%d ", a[i]);
    }
}
 
int main() {
    primeNumberSieve();
    return 0;
}

 

 

참고: 22. 에라토스테네스의 체 : 네이버 블로그 (naver.com)